Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, if the perpendicular bisectors of AB and AD meet at P, then prove that BP = DP.
उत्तर
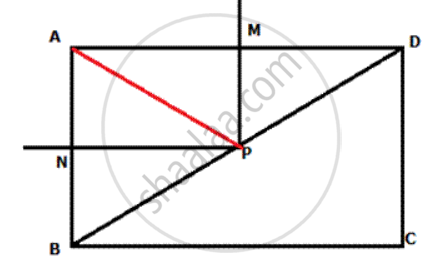
Join A to P.
In Δ AMPand Δ DMP
MP = MP
AM = MD
∠ AMP = ∠ DMP = 90°
Therefore, Δ AMPand Δ DMP are congruent.
DP= AP ....... (i)
In Δ ANP and Δ BNP
NP= NP
AN= NB
∠ANP = ∠BNP = 90°
Therefore, Δ ANP and Δ BNP are congruent.
BP= AP ....... (ii)
From (i) and (ii)
BP= DP
Hence, proved.
APPEARS IN
संबंधित प्रश्न
In each of the given figures; PA = PB and QA = QB.
| i. | 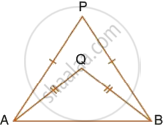 |
| ii. | 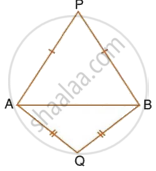 |
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of the points equidistant from two given fixed points.
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
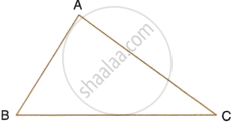
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of points at distances less than 3 cm from a given point.
Describe the locus of points at distances greater than 4 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
Prove that the common chord of two intersecting circles is bisected at right angles by the line of centres.
