Advertisements
Advertisements
प्रश्न
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length f 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
उत्तर १
(I) Draw PQ, the perpendicular bisector of chord AC. PQ is the required locus, which is the diameter of the circle.
Reason: We know each point on the perpendicular bisector of AB is equidistant from A and B. Also the perpendicular bisector of a chord, passes through the centre of the circle and any chord passing through the centre of the circle is its diameter.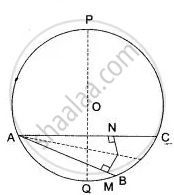
∴ PQ is the diameter of the circle.
(ii) Chords AB and AC intersects at M and N is a moving point such that LM = LN, where LM ⊥ AB and LN ⊥ AC
In right ΔALN and ΔALB
∠ANL = ∠ABL ...(90° each)
AL = AL ...(Common)
NL = BL ...[Given]
∴ ΔALN = ΔALB ...[R.H.S.]
Hence ∠MAL = ∠BAL ...c.p.c.t.
Thus, L lies on the bisector of ∠BAC.
Hence proved.
उत्तर २
Draw a circle of radius 4 cm whose centre is O. Take a point A on the circumference of this circle.
With A as centre and radius 6 cm draw an arc to cut the circumference at B. Join AB.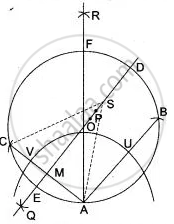
Then AB is the chord of the circle of length 6 cm.
With A as centre and radius 5 cm draw another arc to cut the circumference at C. Join AC then AC is the chord of the circle of length 5 cm.
With A as centre and a suitable radius, draw two arcs on opposite sides of AC.
With C as centre and the same radius, draw two arcs on opposite sides of AC to intersect the former arcs at P and Q.
Join PQ and produce to cut the circle at D and E.
Join DE. Then chord DE is the locus of points inside the circle that Ls equidistant from A and C.
As chord DE passes through (he centre O of the circle, it is a diameter. To prove the construction take any point S inside the circle on DE.
APPEARS IN
संबंधित प्रश्न
Describe the locus of a point P, so that:
AB2 = AP2 + BP2,
where A and B are two fixed points.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. prove your construction.
(ii) Construct the locus of points, inside the circle that are equidistant from AB and AC.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these Iines and also 2 cm away from their point of intersection. How many such points exist?
Construct a rhombus ABCD with sides of length 5 cm and diagonal AC of length 6 cm. Measure ∠ ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
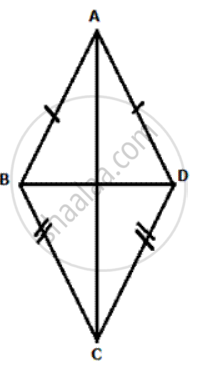
In given figure, ABCD is a kite. AB = AD and BC =CD. Prove that the diagona AC is the perpendirular bisector of the diagonal BD.
Draw and describe the lorus in the following cases:
The Iocus of the mid-points of all parallel chords of a circle.
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
State and draw the locus of a swimmer maintaining the same distance from a lighthouse.
Use ruler and compasses only for the following questions:
Construct triangle BCP, when CB = 5 cm, BP = 4 cm, ∠PBC = 45°.
Complete the rectangle ABCD such that :
(i) P is equidistant from AB and BC and
(ii) P is equidistant from C and D. Measure and write down the length of AB.
