Advertisements
Advertisements
प्रश्न
Ruler and compass only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct Δ ABC, in which BC = 8 cm, AB = 5 cm, ∠ ABC = 60°.
(ii) Construct the locus of point inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark as P, the point which is equidistant from AB, BC and also equidistant from B and C.
(v) Measure and record the length of PB.
उत्तर
(i) Steps of Construction:
1. Draw a line segment BC = 8 cm.
2. Make ∠CBX = 60°
3. Set off BA = 5 cm, along BX.
4. Join CA.
Then, ΔABC is the required triangle.
(ii) We know that the locus of point equidistant from two intersecting straight lines consist of a pair of straight lines that bisect the angles between the given straight lines.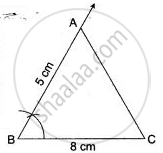
Therefore in this case is the angle bisector of angle B, It is shown in the adjoining figure.
(iii) We know that the locus of a point equidistant from two fixed points is the right bisector of the straight line joining the two fixed points.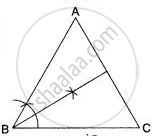
Therefore, in this case the right bisector of side BC of ΔABC. It is shown in the given figure.
(iv) The point P, is the point in intersecting of angle bisector of ∠ABC and the right bisector of BC.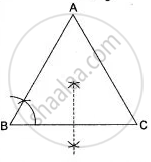
It is shown in the following figure.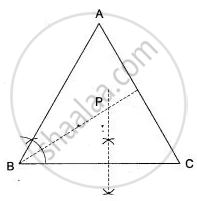
(v) On measuring we find the length of PB = 3 cm.
APPEARS IN
संबंधित प्रश्न
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
Construct a Δ XYZ in which XY= 4 cm, YZ = 5 cm and ∠ Y = 1200. Locate a point T such that ∠ YXT is a right angle and Tis equidistant from Y and Z. Measure TZ.
Draw and describe the lorus in the following cases:
The lorus of a point in rhombus ABCD which is equidistant from AB and AD .
Draw and describe the locus in the following cases :
The locus of a point in the rhombus ABCD which is equidistant from the point A and C
Construct a triangle BPC given BC = 5 cm, BP = 4 cm and .
i) complete the rectangle ABCD such that:
a) P is equidistant from AB and BCV
b) P is equidistant from C and D.
ii) Measure and record the length of AB.
Without using set squares or protractor construct a triangle ABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.
(i) Locate the point P such that ∠BAp = 90° and BP = CP.
(ii) Measure the length of BP.
Using ruler and compasses construct:
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of point equidistant from A and C.
(iii) a circle touching AB at A and passing through C.
Without using set squares or protractor construct:
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Given ∠BAC (Fig), determine the locus of a point which lies in the interior of ∠BAC and equidistant from two lines AB and AC.
