Advertisements
Advertisements
Question
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

Solution
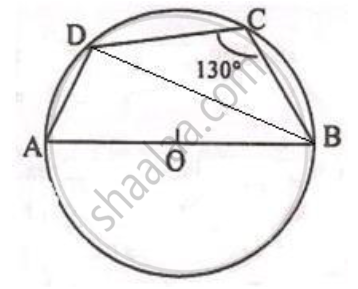
Given: AB is the diameter of the circle with centre O, ∠BCD = 130°
To find: ∠DAB, ∠DBA
1) Clearly, ABCD is a cyclic quadrilateral.
We know, the sum of a pair of opposite angles of a cyclic quadrilateral is 180°
∴ ∠DAB + ∠DCB = 180°
⇒ ∠DAB + 130° = 180°
⇒ ∠DAB = 180° - 130° = 50°
2) Consider ΔDAB,
Here, ∠ADB = 90° …..[Since angle in a semi-circle is a right angle]
So, by angle sum property of a triangle,
∠DAB + ∠DBA + ∠ADB = 180°
⇒ 50° + ∠DBA + 90° = 180°
⇒ ∠DBA = 180° - 140° = 40°
APPEARS IN
RELATED QUESTIONS
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠BCQ =140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
In the following figure, Prove that AD is parallel to FE.

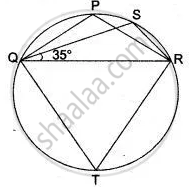
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.