Advertisements
Advertisements
Question
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.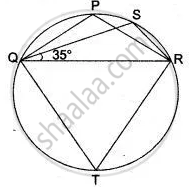
Solution
In ΔPQR, We have
PQ = PR
⇒ ∠ PQR = ∠ PRQ
⇒ ∠ PRQ = 35°
∴ ∠ QPR = 180° - ( ∠ PQR + ∠ PRQ)
∴ ∠ QPR = 180° - ( 35° + 35°) = 110°
Since PQTR is a cyclic quadrilateral.
∴ ∠ P + ∠ T = 180°
∴ ∠ T = 180° - 110° = 70°.
In cyclic quadrilateral QSRT, we have
∴ ∠ S + ∠ T = 180°
⇒ ∠ S = 180° - 70° = 110°.
APPEARS IN
RELATED QUESTIONS
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
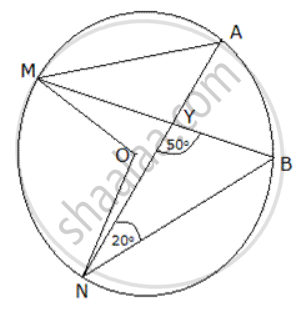
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
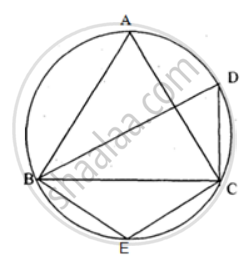
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
