Advertisements
Advertisements
Question
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
Solution
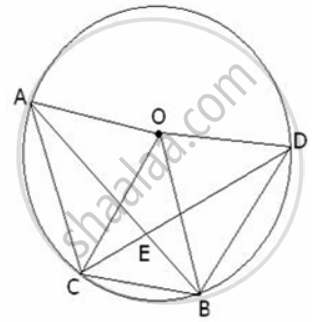
Arc AC subtends LAOC at the centre of circle and LABC on the circumference of the cirde .
∴ ∠ AOC = 2 ∠ ABC ...(1)
Similarly, ∠ BOD and ∠ DCB are the angles subtended by the arc DB at the centre and on the circumference of the circle respectively .
∴ ∠ BOD = 2 ∠ DCB ... (2)
Adding ( 1) and (2),
∠ AOC+ ∠ BOD = 2(∠ ABC + ∠ DCB) ... (3)
In triangle ECB ,
∠ AEC = ∠ ECB + ∠ EBC = ∠ DCB + ∠ ABC
From (3),
∠ AOC+ ∠ BOD = 2 ∠ AEC
Hence Proved.
APPEARS IN
RELATED QUESTIONS
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

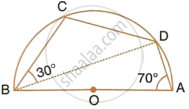
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
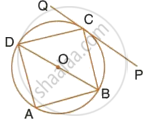
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
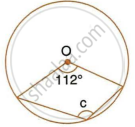
In following fig., O is the centre of the circle. Find ∠ CBD.
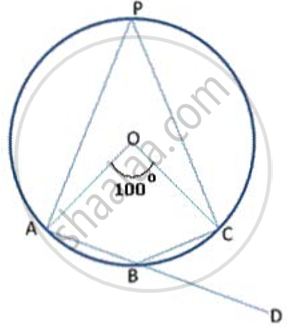
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the following figure, Prove that AD is parallel to FE.

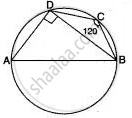
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

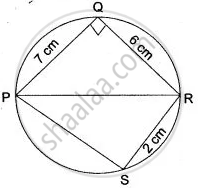
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.