Advertisements
Advertisements
Question
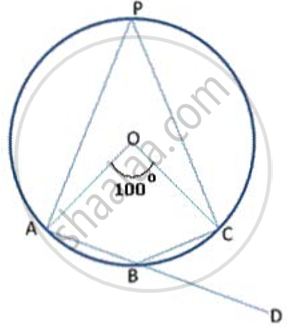
In following fig., O is the centre of the circle. Find ∠ CBD.
Solution
It is given that ∠ AOC = 100°
Arc AC subtends ∠ AOC at the centre of circle and ∠ APC on the circumference of the circle
∴ ∠ AOC = 2 c
⇒ ∠ APC = `(100°)/2` = 50°
It can be seen that APCB is a cyclic quadriIateral.
∴ ∠ APC + ∠ ABC = 180° (Sum of opposite angles of a cyclic quadrilateral)
⇒ ∠ ABC = 180° - 50° = 130°
Now , ∠ ABC + ∠ CBD = 180° (Linear pair angles)
∠ CBD = 180° - 130° = 50°
APPEARS IN
RELATED QUESTIONS
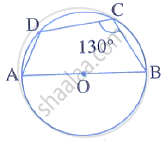
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
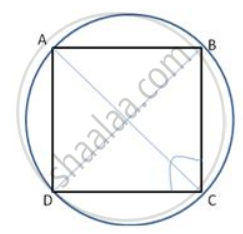
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

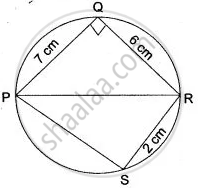
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.