Advertisements
Advertisements
Question
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
Solution

m ∠ A = 3 (m ∠C)
∠ A + ∠ C = 180 (Opposite angles of a cyclic quadrilateral)
3∠C + ∠ C = 180
4 ∠ C = 180
∠ C = 45
m ∠ A = 3 (m ∠ C)
= 3 × 45
= 135
m ∠ A = 135°
APPEARS IN
RELATED QUESTIONS
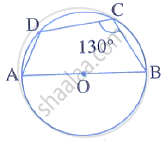
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
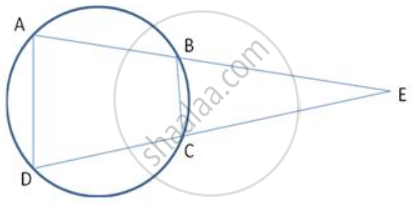
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
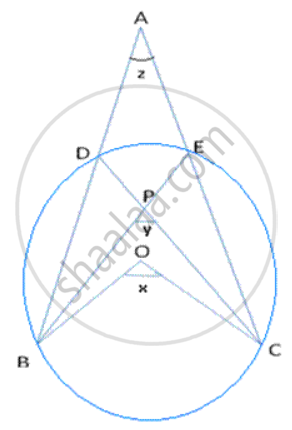
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.