Advertisements
Advertisements
Question
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
Solution
Let ∠A and ∠C be 3x and x respectively
In cyclic quadrilateral ABCD,
∠A + ∠C = 180°
(Pairs of opposite angles in a cyclic quadrilateral are supplementary)
`=>` 3x + x = 180°
`=> x = (180^circ)/4 = 45^circ`
∴ ∠A = 135° and ∠C = 45°
Let the measure of ∠B and ∠D be y and 5y respectively
In cyclic quadrilateral ABCD,
∠B + ∠D = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary are supplementary)
`=>` y + 5y = 180°
`=> y = (180^circ)/6 = 30^circ`
∴ ∠B = 30° and ∠D = 150°
APPEARS IN
RELATED QUESTIONS
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
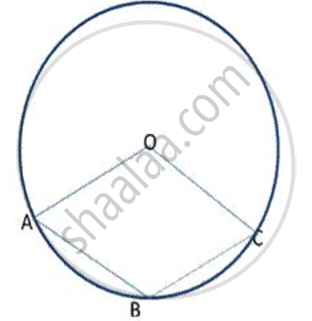
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
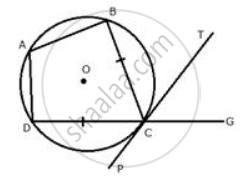
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
If O is the centre of the circle, find the value of x in each of the following figures
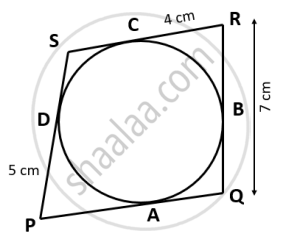
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: