Advertisements
Advertisements
Question
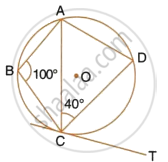
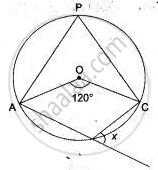
If O is the centre of the circle, find the value of x in each of the following figures
Solution
APC = `1/2"AOC" = 1/2 xx 120°` = 60°
Since ABCD is a cyclic quadrilateral.
CBD = x is the exterior angle
So, x = APC = 60°.
APPEARS IN
RELATED QUESTIONS
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
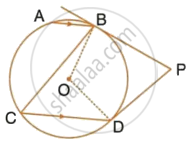
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
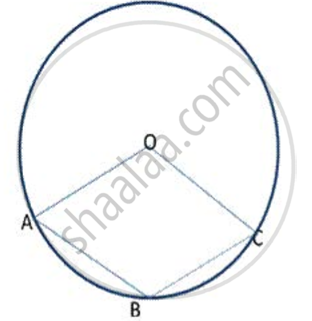
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
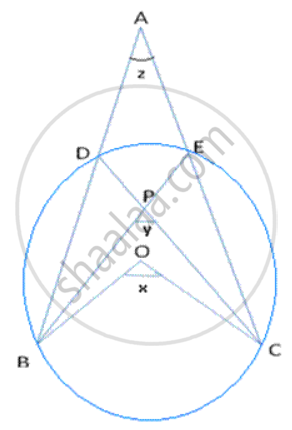
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
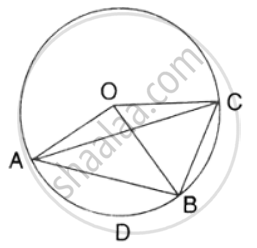
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
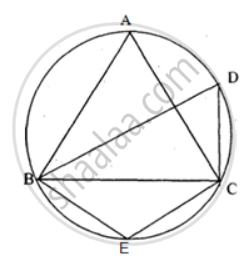
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.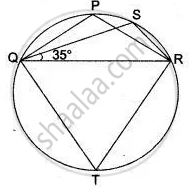
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.