Advertisements
Advertisements
प्रश्न
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
उत्तर
Let ∠A and ∠C be 3x and x respectively
In cyclic quadrilateral ABCD,
∠A + ∠C = 180°
(Pairs of opposite angles in a cyclic quadrilateral are supplementary)
`=>` 3x + x = 180°
`=> x = (180^circ)/4 = 45^circ`
∴ ∠A = 135° and ∠C = 45°
Let the measure of ∠B and ∠D be y and 5y respectively
In cyclic quadrilateral ABCD,
∠B + ∠D = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary are supplementary)
`=>` y + 5y = 180°
`=> y = (180^circ)/6 = 30^circ`
∴ ∠B = 30° and ∠D = 150°
APPEARS IN
संबंधित प्रश्न
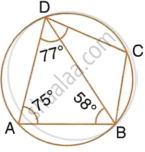
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
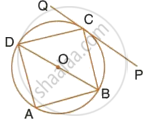
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
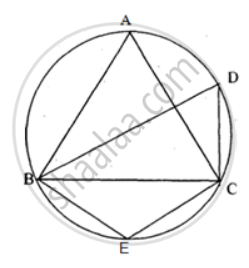
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.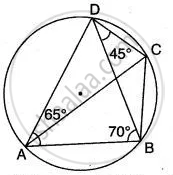
In the given figure O is the center of the circle, ∠ BAD = 75° and chord BC = chord CD. Find:
(i) ∠BOC (ii) ∠OBD (iii) ∠BCD.