Advertisements
Advertisements
प्रश्न
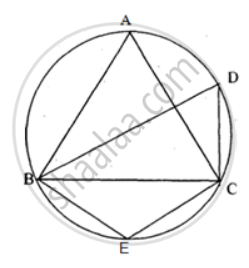
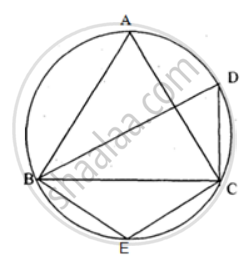
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
उत्तर
In cyclic quadrialteral ABEC,
∠BAC + ∠BEC = 180°
⇒ ∠BAC + 148° = 180°
⇒ ∠BAC = 180° - 148°
⇒ ∠BAC = 32°
APPEARS IN
संबंधित प्रश्न
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

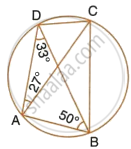
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
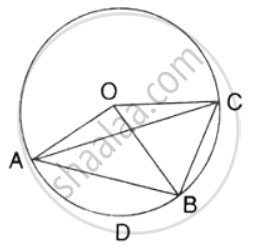
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
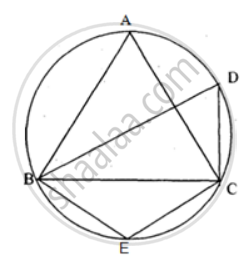
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.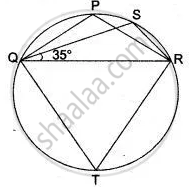
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.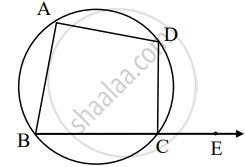
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
