Advertisements
Advertisements
प्रश्न
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
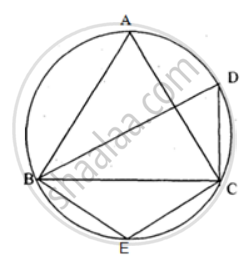
उत्तर
We know that the opposite angles of a cyclic quadrilateral are supplementary.
Thus, in cyclic quadrilateral BECD ,
∠ BEC + ∠ BDC = 180°
⇒ ∠ BEC + 32° = 180°
⇒ ∠ BEC = 180° - 32°
⇒ ∠ BEC = 148°
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

Use the given figure to find:
- ∠BAD,
- ∠DQB.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
In the following figure, Prove that AD is parallel to FE.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.