Advertisements
Advertisements
प्रश्न
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
उत्तर

m ∠ A = 3 (m ∠C)
∠ A + ∠ C = 180 (Opposite angles of a cyclic quadrilateral)
3∠C + ∠ C = 180
4 ∠ C = 180
∠ C = 45
m ∠ A = 3 (m ∠ C)
= 3 × 45
= 135
m ∠ A = 135°
APPEARS IN
संबंधित प्रश्न
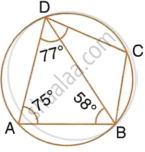
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
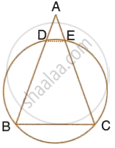
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
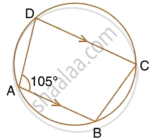
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In the figure, given below, find: ∠ADC, Show steps of your working.
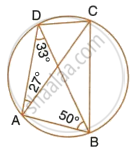
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
In the following figure, Prove that AD is parallel to FE.

