Advertisements
Advertisements
प्रश्न
In the figure, given below, find: ∠ADC, Show steps of your working.
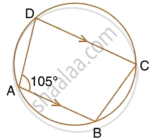
उत्तर
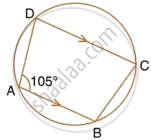
Now, AB || CD
∴ ∠BAD + ∠ADC = 180°
(Interior angles on the same side of parallel lines is 180°)
`=>` ∠ADC = 180° – 105° = 75°
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

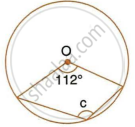
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
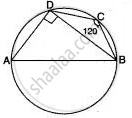
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.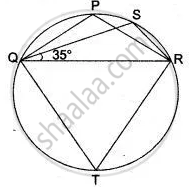
In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.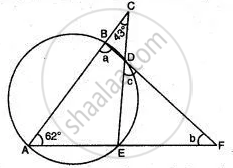
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.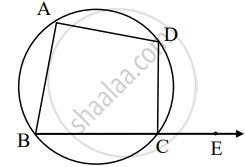
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
