Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
उत्तर
Given: ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawn that it intersect AD at P and BC at Q. To prove points P, Q, C and D are con-cyclic.
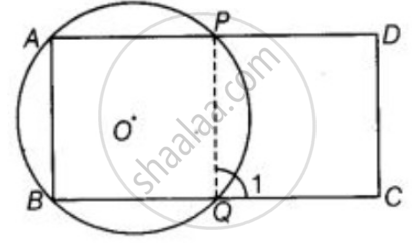
Construction: Join PQ
Proof: ∠1 = ∠A ...[Exterior angle property of cyclic quadrilateral]
But ∠A = ∠C ...[Opposite angles of a parallelogram]
∴ ∠1 = ∠C ...(i)
But ∠C + ∠D = 180° ...[Sum of cointerior angles on same side is 180°]
`=>` ∠1 + ∠D = 180° ...[From equation (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q, C and D are con-cyclic.
Hence proved.
APPEARS IN
संबंधित प्रश्न
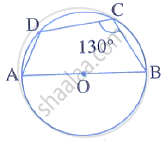
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
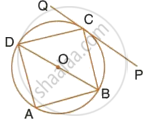
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
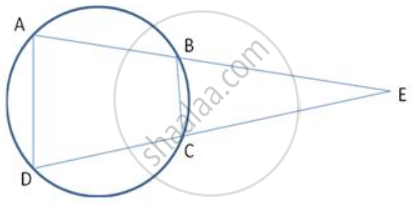
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
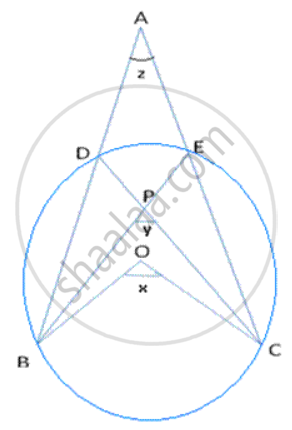
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC
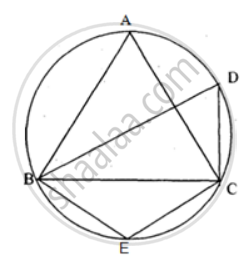
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
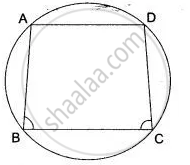
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
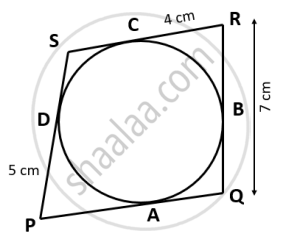
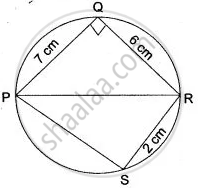
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: