Advertisements
Advertisements
प्रश्न
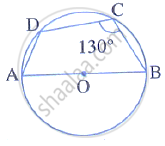
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
उत्तर
i. ABCD is a cyclic quadrilateral
m∠DAB = 180° − ∠DCB
= 180° - 130°
= 50°
ii. In ∆ADB,
m∠DAB + m∠ADB + m∠DBA = 180°
⇒ 50° + 90° + m∠DBA = 180°
⇒ m∠DBA = 40°
APPEARS IN
संबंधित प्रश्न
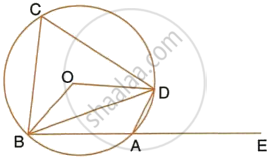
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD
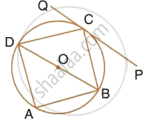
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find;
- ∠DBC
- ∠BCP
- ∠ADB
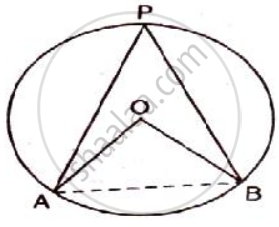
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
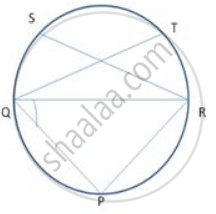
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR
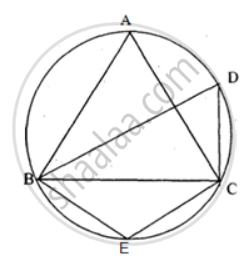
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
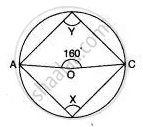
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
