Advertisements
Advertisements
प्रश्न
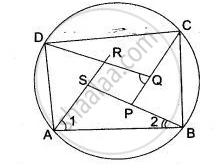
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
उत्तर
Given: In cyclic ABCD the bisectors formed a quadrilateral ABCD.
To prove: PQRS is a cyclic quadrilateral.
Proof: In cyclic quadrilateral ABCD, AR and BS be the bisectors of ∠A and ∠B.
So, ∠ 1 = ∠ A/2 and ∠ 2 = ∠ B/2
In Δ ASB, ∠ RSP is the exterior angle
So ∠ RSP = ∠1 + ∠2
∠ RSP = `"∠A"/2 + "∠B"/2` ....(i)
Similarly, ∠ PQR = `"∠C"/2 + "∠D"/2` ....(ii)
Adding (i) and (ii),
∠ PQR + ∠ RSP = `1/2`(∠A + ∠B + ∠C + ∠D)
= `1/2` x 360° = 180°
∠ PQR + ∠ RSP = 180°
But these are the opposite angles of quadrilateral PQRS
Hence PQRS is a cyclic quadrilateral.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

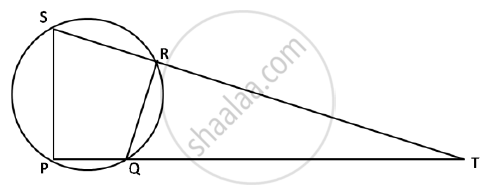
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
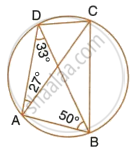
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.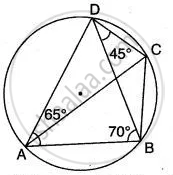
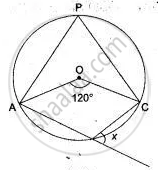
If O is the centre of the circle, find the value of x in each of the following figures
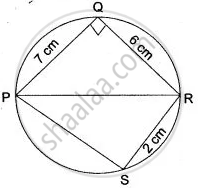
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.