Advertisements
Advertisements
प्रश्न
Two chords of lengths 10cm and 24cm are drawn parallel o each other in a circle. If they are on the same side of the centre and the distance between them is 17cm, find the radius of the circle.
उत्तर
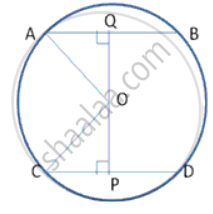
CP = PO = 12cm
Let OA = OC = r (say)
Also, let OQ = x, ∴ OP = 17 - x
In right Δ OPC,
By Pythagoras theorem,
OC2 = OP2 + PC2
r2 = (17- x)2 + 122 ----( 1 )
Similarly, In Δ OQA,
OA2 = AQ2 + QO2
r2 = 52 + x2 ----(2}
From (1) and { 2}
( 17 - x)2 + 122 = 52 + x2
289 - 34 x + 144 - 25 = 0
34x = 408
x = 12
From {2}
r2 = 52 + 122
25+ 144= 169
r = 13
The radius of the circle is 13cm .
APPEARS IN
संबंधित प्रश्न
A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
A chord of length 24 cm is at a distance of 5 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.
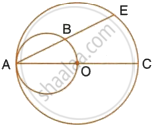
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
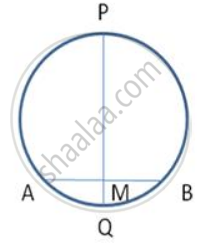
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y : express ∠ABD in terms of y.

In the following figure; P and Q are the points of intersection of two circles with centers O and O'. If straight lines APB and CQD are parallel to OO';
prove that: (i) OO' = `1/2`AB ; (ii) AB = CD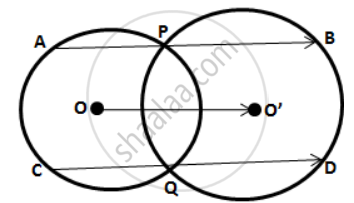
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.
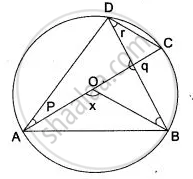
In the figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q, r in term of x.

