Advertisements
Advertisements
Question
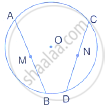
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.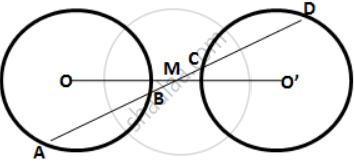
Solution
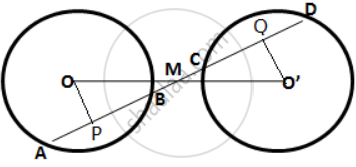
Given: A straight line AD intersects two circles of equal radii at A, B, C and D.
The line joining the centers OO' intersect AD at M and M is the midpoint of OO'.
To Prove: AB = CD.
Construction: From O, draw OP ⊥ AB and from O', draw O'Q ⊥ CD.
Proof:
In ΔOMP and ΔO'MQ,
∠OMP = ∠O'MQ ...( Vertically Opposite angles )
∠OPM = ∠O'QM ...( each = 90° )
OM = O'M ...( Given )
By Angle-Angle-Side criterion of congruence,
∴ ΔOMP ≅ ΔO'MQ, ...( by AAS )
The corresponding parts of the congruent triangles are congruent.
∴ OP = O'Q ...( c.p.c.t. )
We know that two chords of a circle or equal circles which are equidistant from the center are equal.
∴ AB = CD.
APPEARS IN
RELATED QUESTIONS
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the area of the rhombus is `32sqrt(3) cm^2` find the radius of the circle.
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
In fig, AB and CD are two equal chords of a circle with centre O. If M and N are the midpoints of AB and CD respectively,
prove that (a) ∠ ONM = ∠ ONM (b) ∠ AMN = ∠ CNM.
AB and AC are two equal chords of a circle with centre o such that LABO and LCBO are equal. Prove that AB = BC.
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD