Advertisements
Advertisements
Question
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
Solution
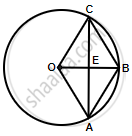
Radius = 10 cm
In rhombus OABC,
OC = 10 cm
∴ `OE = 1/2 xx OB`
= `1/2 xx 10`
= 5 cm
In right ΔOCE,
OC2 = OE2 + EC2
`=>` 102 = 52 + EC2
`=>` EC2 = 100 – 25 = 75
`=>` EC = `5sqrt(3)`
∴ AC = 2 × EC
= `2 xx 5sqrt(3)`
= `10sqrt(3)`
Area of rhombus = `1/2 xx OB xx AC`
= `1/2 xx 10 xx 10sqrt(3)`
= `50 sqrt(3) cm^2 ≈ 86.6 cm^2` ...`(sqrt(3) = 1.73)`
APPEARS IN
RELATED QUESTIONS
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
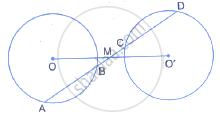
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
In fig, AB and CD are two equal chords of a circle with centre O. If M and N are the midpoints of AB and CD respectively,
prove that (a) ∠ ONM = ∠ ONM (b) ∠ AMN = ∠ CNM.
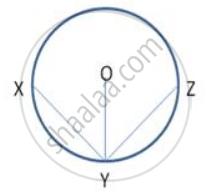
In following figure .,XY and YZ are two equal chords of a circle with centre O. Prove that the bisector of ∠ XYZ passes through O.
In fig., chords AB and CD of a circle intersect at P. AP = 5cm, BP= 3cm and CP = 2.5cm. Determine the length of DP.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.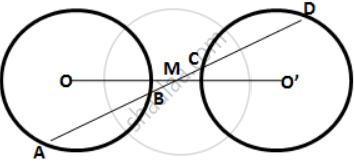
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP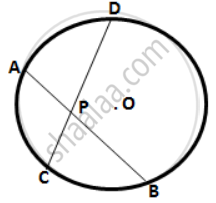
Prove that equal chords of congruent circles subtend equal angles at their center.
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD
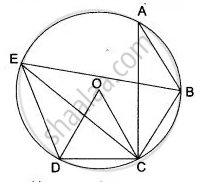
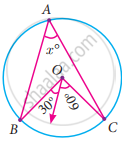
Find the value of x° in the following figure: