Advertisements
Advertisements
Question
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Solution
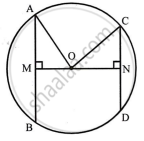
Given: A circle with centre O and radius r. OM ⊥ AB and ON ⊥ CD Also AB > CD
To prove: OM < ON
Proof: Join OA and OC.
In right ΔAOM,
AO2 = AM2 + OM2
`=> r^2 = (1/2 AB)^2 + OM^2`
`=> r^2 = 1/4 AB^2 + OM^2` ...(i)
Again in right ΔONC,
OC2 = NC2 + ON2
`=> r^2 = (1/2 CD )^2 + ON^2`
`=> r^2 = 1/4 CD^2 + ON^2` ...(ii)
From (i) and (ii)
`1/4 AB^2 + OM^2 = 1/4 CD^2 + ON^2`
But, AB > CD ...(Given)
∴ ON > OM
`=>` OM < ON
Hence, AB is nearer to the centre than CD.
APPEARS IN
RELATED QUESTIONS
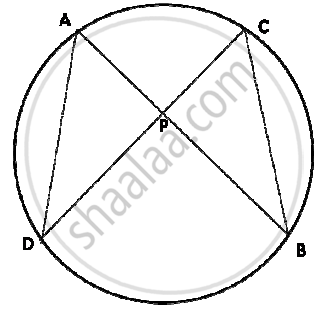
AB and CD are two chords of a circle intersecting at P. Prove that AP x PB = CP x PD
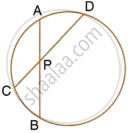
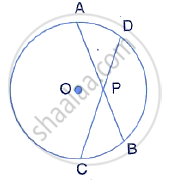
In the given figure 3 × CP = PD = 9 cm and AP = 4.5 cm. Find BP.
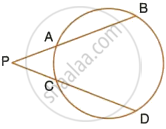
In the given figure, 5 × PA = 3 × AB = 30 cm and PC = 4 cm. Find CD.
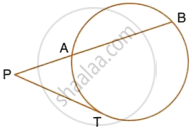
In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.
Chords AB and CD of a circle intersect each other at point P such that AP = CP
Show that: AB = CD
In two concentric circles, prove that all chords of the outer circle, which touch the inner circle, are of equal length.
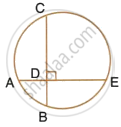
In the given figure, AE and BC intersect each other as point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.
Two tangents are drawn to a circle from an external point P. touching the circle at the points A and B. A third tangent intersects segment PA in C and segment PB in D and touches the circle at Q. if PA = 20 units, find the perimeter of Δ PCD.
If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.
Two circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12 cm. Find the distance between their centres.
