Advertisements
Advertisements
Question
AB and CD are two chords of a circle intersecting at P. Prove that AP x PB = CP x PD
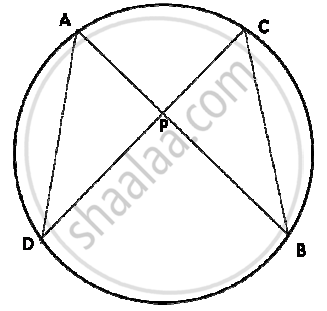
Solution
Construction: Join AD and CB.
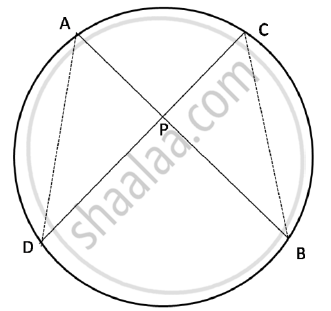
In ΔAPD and ΔCPB
∠A = ∠C .....(Angles in the same segment)
∠D = ∠B .....(Angles in the same segment)
⇒ ΔAPD ~ ΔCPB ...(By AA Postulate)
`=> (AP)/(CP) = (PD)/(PB)` ...(Corresponding sides of similar triangles)
`=> AP xx PB = CP xx PD`
APPEARS IN
RELATED QUESTIONS
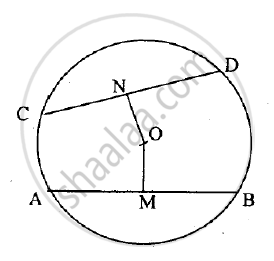
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.
AB = 24 cm, OM= 5 cm, ON= 12 cm. Find the:
1) radius of the circle
2) length of chord CD.
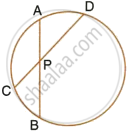
In the given figure 3 × CP = PD = 9 cm and AP = 4.5 cm. Find BP.
In the given figure, 5 × PA = 3 × AB = 30 cm and PC = 4 cm. Find CD.
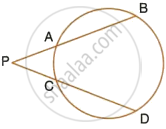
In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.
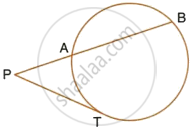
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Chords AB and CD of a circle intersect each other at point P such that AP = CP
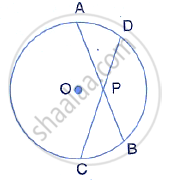
Show that: AB = CD
In two concentric circles, prove that all chords of the outer circle, which touch the inner circle, are of equal length.
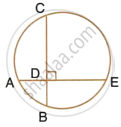
In the given figure, AE and BC intersect each other as point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.
Two tangents are drawn to a circle from an external point P. touching the circle at the points A and B. A third tangent intersects segment PA in C and segment PB in D and touches the circle at Q. if PA = 20 units, find the perimeter of Δ PCD.
If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.
