Advertisements
Advertisements
Question
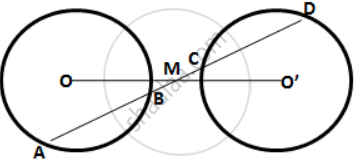
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
Solution
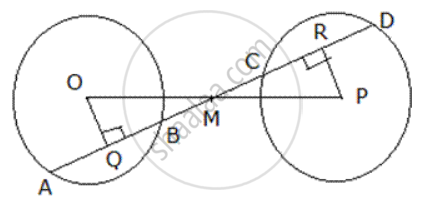
Given: Two congruent circles with centre 0 and P. Mis the mid-point of OP
To prove: Chord AB and CD are equal.
Construction: Draw OQ ⊥ AB and PR ⊥ CD.
Proof: In Δ OQM and Δ PRM
∠ OQM = ∠ PRC ...(Each 90°)
OM =MP ....(As M is the mid-point)
∠OMQ = ∠ PMR ...(Verically opposite angles)
Therefore, Δ OQM ≅ ΔPRM
⇒ OQ = PR ...(By CPCT)
Now the perpendicular distances of two chords 1n two congruent circles are equal, therefore chords are also equal.
⇒ AB = CD
Hence proved.
APPEARS IN
RELATED QUESTIONS
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
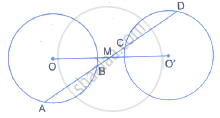
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
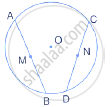
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
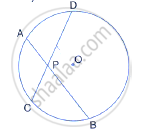
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
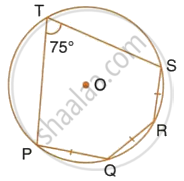
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
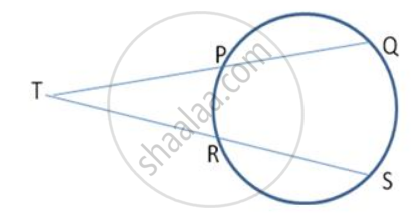
In fig, AB and CD are two equal chords of a circle with centre O. If M and N are the midpoints of AB and CD respectively,
prove that (a) ∠ ONM = ∠ ONM (b) ∠ AMN = ∠ CNM.
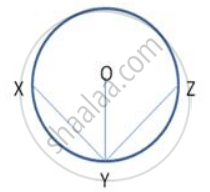
In following figure .,XY and YZ are two equal chords of a circle with centre O. Prove that the bisector of ∠ XYZ passes through O.
AB and AC are two equal chords of a circle with centre o such that LABO and LCBO are equal. Prove that AB = BC.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.