Advertisements
Advertisements
Question
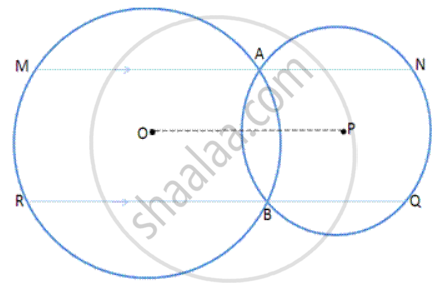
Two circles with centres O and P intersect each other at A and B as shown in following fig. Two straight lines MAN and RBQ are drawn parallel to OP.
Prove that (i) MN = 20 P (ii) MN= RQ.
Solution
Given: Two cirdes with centres 0 and P, and MN II OP || RQ
To prove: (i) MN = 20P (ii) MN= RQ.
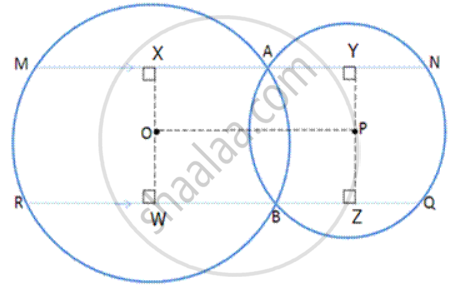
Construction: OX ⊥ MN, PY ⊥ MN, OW ⊥ RZ, PZ ⊥ RQ
Proof: Since each angle of the quadrilateral XYZW is a right angle, sc XYZW is a rectangle.
Also, XYPO is a rectangle. ...(1)
Now, perpendicular drawn from the centre to the chord bisects the chord.
Therefore, MA = 2 XA and AN = 2 AY ...(2)
Now, MN = MA + AN = 2 XA + 2 AY [from (2)]
⇒ MN = 2(XA + AY) = 2 XY
⇒ MN = 2 OP [As XYPO is a rectangle, XY = OP] ... (3)
This proves part (i).
By similar arguments, we have RQ = 2 OP ...(4)
Using (3) and ( 4), we get
MN= RQ.
This proves part (ii).
APPEARS IN
RELATED QUESTIONS
Two circle touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centres if:
- they touch each other externally,
- they touch each other internally.
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:

(ii) angles APB = 90°
Two circle with centres O and O' are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. Prove that OA bisects angle BAC.

Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that ∠CPA = ∠DPB.
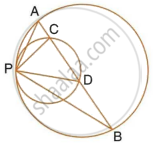
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD.
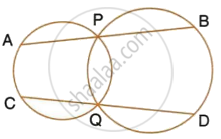
In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.
Radius of a sector of a circle is 21 cm. If length of arc of that sector is 55 cm, find the area of the sector.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if -
they touch each other internally.
P and Q are the centre of circles of radius 9 cm and 2 cm respectively; PQ = 17 cm. R is the centre of circle of radius x cm, which touches the above circles externally, given that ∠ PRQ = 90°. Write an equation in x and solve it.
