Advertisements
Advertisements
Question
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
Solution
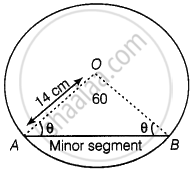
Given that, radius of circle (r) = 14 cm
And angle of the corresponding sector i.e., central angle (θ) = 60°
Since, in ΔAOB, OA = OB = Radius of circle i.e., ΔAOB is isosceles.
⇒ ∠OAB = ∠OBA = θ
Now, in ΔOAB,
∠AOB + ∠OAB = ∠OBA = 180° ...[Since, sum of interior angles of any triangle is 180°]
⇒ 60° + θ + θ = 180° ...[Given, ∠AOB = 60°]
⇒ 2θ = 120°
⇒ θ = 60°
i.e. ∠OAB = ∠OBA = 60° = ∠AOB
Since, all angles of ΔAOB are equal to 60° i.e., ΔAOB is an equilateral triangle.
Also, OA = OB = AB = 14 cm
So, Area of ΔOAB = `sqrt(3)/4` (side)2
= `sqrt(3)/4 xx (14)^2` ...[∵ Area of an equilateral triangle = `sqrt(3)/4` (sides)2]
= `sqrt(3)/4 xx 196`
= `49sqrt(3) "cm"^2`
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
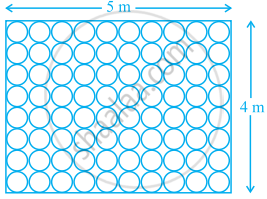
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
