Advertisements
Advertisements
Question
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Solution
The statement is false because the area of a sector of a circle = `(1/2)"r"^2θ`, where r is the radius and θ the angle in radians subtended by the arc at the center of the circle.
It does not depend on the arc length.
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
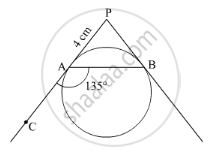
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°.
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
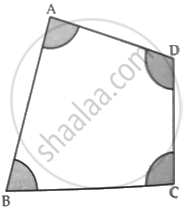
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.