Advertisements
Advertisements
Question
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
Solution
Length of arc, S = 8 cm
Radius of circle, r = 3 cm
`"S" = rθ ⇒ θ = "S"/r = 8/3`radians
`8/3"radians"=180/pixx8/3=(480/pi)@`
`"Area of the sector "=theta/360xxpir^2=480/(360xxpi)xxpir^2=4/3xx9=12"cm"^2`
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

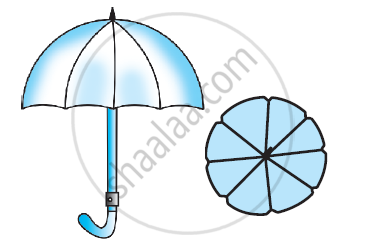
An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
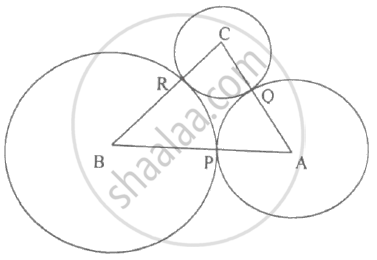
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
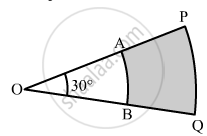
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
