Advertisements
Advertisements
Question
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
Solution
According to the question,
The four circles are placed such that each piece touches the other two pieces.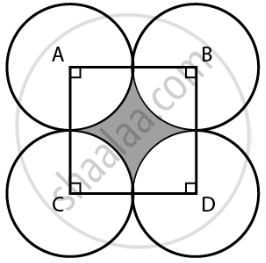
By joining the centres of the circles by a line segment, we get a square ABDC with sides,
AB = BD = DC = CA = 2 ...(Radius)
= 2(7) cm
= 14 cm
Now, Area of the square = (Side)2
= (14)2
= 196 cm2
ABDC is a square,
Therefore, each angle has a measure of 90°.
i.e., ∠A = ∠B = ∠D = ∠C = 90° = `pi/2` radius = θ ...(say)
Given that,
Radius of each sector = 7 cm
Area of the sector with central angle A = `(1/2)"r"^2θ`
= `1/2"r"^2θ`
= `1/2 xx 49 xx pi/2`
= `1/2 xx 49 xx 22/(2 xx 7)`
= `77/2 "cm"^2`
Since the central angles and the radius of each sector are same, area of each sector is `77/2 "cm"^2`
∴ Area of the shaded portion = Area of square – Area of the four sectors
= `196 - (4 xx 77/2)`
= 196 – 154
= 42 cm2
Therefore, the required area of the portion enclosed between these pieces is 42 cm2.
APPEARS IN
RELATED QUESTIONS
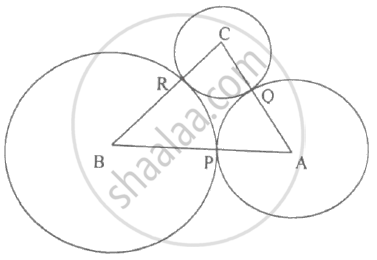
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.

The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Find the perimeter of a quadrant of a circle of radius 14 cm.
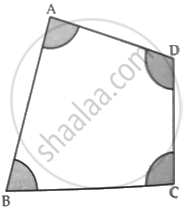
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.