Advertisements
Advertisements
Question
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Solution
Let the central angle of the sector be θ.
Given that, radius of the sector of a circle (r) = 5 cm
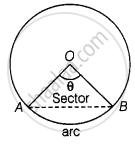
And arc length `(l)` = 3.5 cm
∴ Central angle of the sector,
θ = `("arc length" (l))/"radius"`
⇒ θ = `3.5/5` = 0.7R ...`[∵ θ = l/"r"]`
⇒ θ = `(0.7 xx 180/pi)^circ` ...`[∵ 1"R" = 180^circ/pi "D"^circ]`
Now, area of sector with angle θ = 0.7
= `(pi"r"^2)/360^circ xx (0.7) xx 180^circ/pi`
= `(5)^2/2 xx 0.7`
= `(25 xx 7)/(2 xx 10)`
= `175/20`
= 8.75 cm2
Hence, the required area of the sector of a circle is 8.75 cm2.
APPEARS IN
RELATED QUESTIONS
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
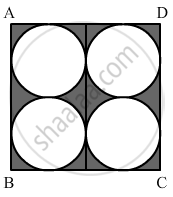
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
