Advertisements
Advertisements
Question
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
Solution
The largest area of the circle is possible when,
diameter = 42
Therefore, radius = `42/2` = 21 cm
Therefore, Area of circle = π × (21)2
= 1386
Area of the rectangle = 55 × 42 = 2310 cm2
Therefore, area of remaining cardboard-
`= 42 xx 55 - pi (21)^2`
`= 42 xx 55 - 22/7 (21)^2`
= 2310 - 1386
= 924
Hence, the volume of the circle and area remaining cardboard-
= 1386 : 924
= 231 : 154
= 3 : 2
APPEARS IN
RELATED QUESTIONS
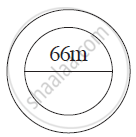
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
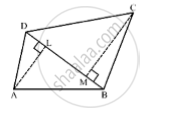
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
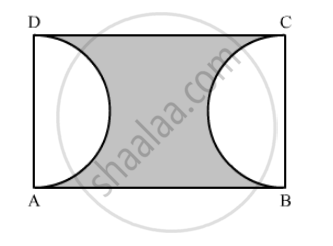
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
In the following figure, the shaded area is

In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

Diameter of a circular garden is 9.8 m. Find its area.
The circumference of a circular park is 352 m. Find the area of the park
The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
