Advertisements
Advertisements
प्रश्न
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
उत्तर
The largest area of the circle is possible when,
diameter = 42
Therefore, radius = `42/2` = 21 cm
Therefore, Area of circle = π × (21)2
= 1386
Area of the rectangle = 55 × 42 = 2310 cm2
Therefore, area of remaining cardboard-
`= 42 xx 55 - pi (21)^2`
`= 42 xx 55 - 22/7 (21)^2`
= 2310 - 1386
= 924
Hence, the volume of the circle and area remaining cardboard-
= 1386 : 924
= 231 : 154
= 3 : 2
APPEARS IN
संबंधित प्रश्न
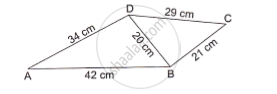
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
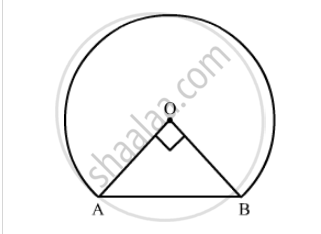
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
The area of the circle that can be inscribed in a square of side 10 cm is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
