Advertisements
Advertisements
Question
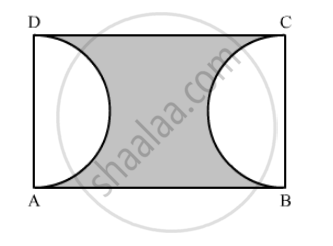
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
Solution
We have given two semi-circles and a rectangle.
Area of the shaded region = Area of the rectangle − Area of the two semicircles
`∴ "Area of the shaded region" =20xx14-2xx1/2xxpixx7xx7`
Substituting pi=`22/7` we get,
`∴ "Area of the shaded region"=20xx14-2xx1/2xx22/7xx7xx7`
`∴ "Area of the shaded region"=20xx14-22xx7`
`∴ "Area of the shaded region"280-154`
`∴ "Area of the shaded region"=126`
Therefore, area of shaded region is `126 cm^2`
APPEARS IN
RELATED QUESTIONS
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
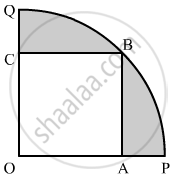
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
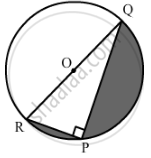
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
Find the area of the shaded region: