Advertisements
Advertisements
Question
A wire is bent to form a square enclosing an area of 484 cm2. Using the same wire, a circle is formed. Find the area of the circle.
Solution
Area of the square = 484 cm2
Area of the square = Side2
⇒ 484 = Side2
222 = Side
Perimeter of the square = 4 Side
Perimeter of the square = 4 × 22 = 88 cm
Length of the wire = 88 cm
Circumference of the circle = Length of the wire = 88 cm
Now, let the radius of the circle be r cm.
Thus, we have:
2πr = 88
`=> 2 xx 22/7 xx r = 88`
⇒ r = 14
Area of the circle = πr2
`=> 22/7xx14xx14`
= 616 x m2
Thus, the area enclosed by the circle is 616 cm2.
APPEARS IN
RELATED QUESTIONS
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
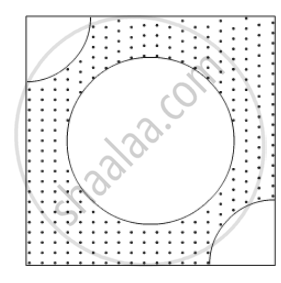
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
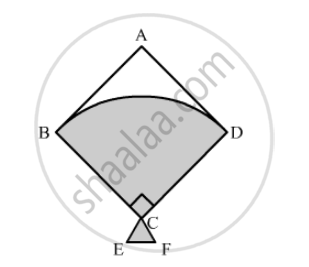
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
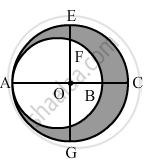
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
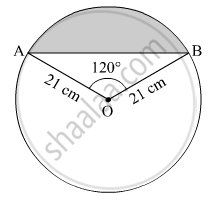
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
Find the area of a circle of radius 30 cm (use π = 3.14).
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
