Advertisements
Advertisements
Question
A square ABCD is inscribed in a circle of radius r. Find the area of the square.
Solution
Let the diameter of the square be d and having circumscribed circle of radius r.
We know that if a circle circumscribes a square, then the diameter of the circle is equal to the diagonal of the square.
∴ d = 2r
Now,
Area of square`=1/2"d"^2 = 1/2(2"r")^2=2"r" "sq"` units
Hence, the area of the square ABCD is 2r2 sq units.
APPEARS IN
RELATED QUESTIONS
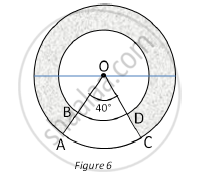
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
A horse is placed for grazing inside a rectangular field 40m by 36m and is tethered to one corner by a rope 14m long. Over how much area can it graze.
The sum of the radii of two circles is 140 cm and the difference of their circumferences in 88 cm. Find the diameters of the circles.
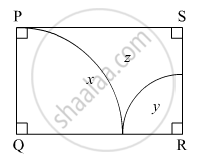
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
The diameter of a wheel is 84 cm. How many revolutions will it make to cover 792 m?
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
Each wheel of a car is of diameter 80 cm. How many completer revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?
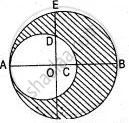
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.