Advertisements
Advertisements
Question
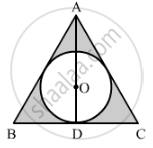
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
Solution
We can find the radius of the incircle by using the formula
`"r" = 2xx"Area of triangle"/"Perimeter of triangle" = (2xxsqrt(3)/4xx(12)^2)/(3xx12) = 2sqrt(3) "cm"`
Now, area of shaded region = Area of triangle - Area of circle
`= sqrt(3)/4xx(12)^2-3.14xx(2sqrt(3))^2`
=62.28-37.68
= 24.6 cm2
Hence, the area of shaded region is 24.6 cm2
APPEARS IN
RELATED QUESTIONS
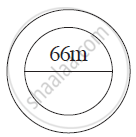
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
There is a path of uniform width 7 m round and outside a circular garden of diameter 210 m. Find the area of the path.
Find the area enclosed between two concentric circles, If their radii are 6cm and 13cm respectively.
The area of a circle is 154 cm2. Its diameter is ____________.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
Find the area of the shaded region: