Advertisements
Advertisements
प्रश्न
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
उत्तर
Area of Square = 196 cm2
Side of Square = `sqrt("Area")` = `sqrt(196)` = 14 cm
Perimeter of Square = 4 x 14 cm
i.e. length of wire = 56 cm
Circumference of circle = 56 cm
2πr = 56
`2 xx 22/7 xx r = 56`
`r = (56 xx 7)/(2 xx 22)`
`r = 98/11` cm
`therefore "Area of circle enclosed" = pir^2`
= `22/7 xx 98/11 xx 98/11`
= `2744/11`
= 249.45 cm2
APPEARS IN
संबंधित प्रश्न
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

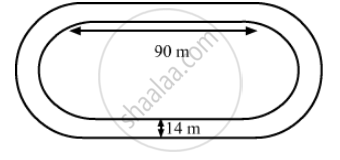
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
