Advertisements
Advertisements
प्रश्न
The radius of a circular wheel is 42 cm. Find the distance travelled by it in :
(i) 1 revolution ;
(ii) 50 revolutions ;
(iii) 200 revolutions ;
उत्तर
(i)
Radius of wheel, r = 42 cm
Circumference i.e. distance travelled in 1 revolution = 2πr = 2 x 22/7 x 42 = 264 cm
(ii)
Distance travelled in 50 revolutions = 264 x 50 = 13200 cm = 132 m
(iii)
Distance travelled in 200 revolutions = 264 x 200 = 52800 cm = 528 m
Hence (i) 264 cm (ii) 132 m (iii) 528 m
APPEARS IN
संबंधित प्रश्न
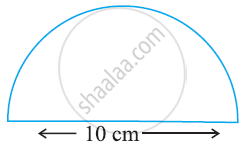
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

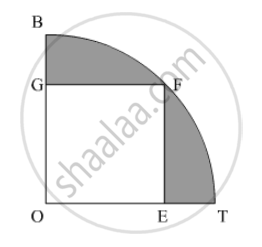
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
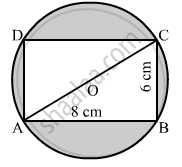
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
The cost of fencing a circular field at the rate of Rs 25 per metre is Rs 5500. The field is to be ploughed at the rate of 50 paise per m2 . Find the cost of ploughing the field. [Take `π =22/7`].
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
