Advertisements
Advertisements
प्रश्न
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
उत्तर
Area of Square = 196 cm2
Side of Square = `sqrt("Area")` = `sqrt(196)` = 14 cm
Perimeter of Square = 4 x 14 cm
i.e. length of wire = 56 cm
Circumference of circle = 56 cm
2πr = 56
`2 xx 22/7 xx r = 56`
`r = (56 xx 7)/(2 xx 22)`
`r = 98/11` cm
`therefore "Area of circle enclosed" = pir^2`
= `22/7 xx 98/11 xx 98/11`
= `2744/11`
= 249.45 cm2
APPEARS IN
संबंधित प्रश्न
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
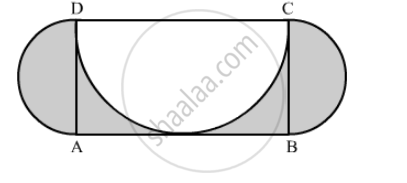
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
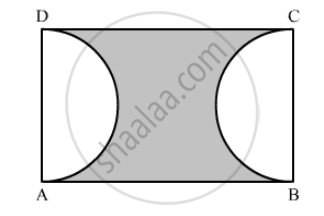
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
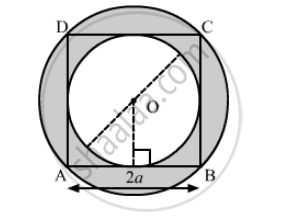
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
