Advertisements
Advertisements
प्रश्न
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
उत्तर
Dimension of the rectangular card board = 14 cm × 7 cm
Since, two circular pieces of equal radii and maximum area touching each other are cut from the rectangular card board, therefore, the diameter of each of each circular piece is 14/2 = 7 cm.
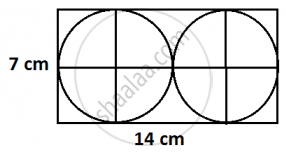
Radius of each circular piece = `7/2`cm
∴ Sum of area of two circular pieces==`2xxpi(7/2)^2=2xx22/7xx49/7=77 cm^2`
Area of the remaining card board = Area of the card board − Area of two circular pieces
= 14 cm × 7 cm − 77 cm2 = 98 cm2 − 77 cm2 = 21 cm2
Thus, the area of the remaining card board is 21 cm2.
APPEARS IN
संबंधित प्रश्न
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
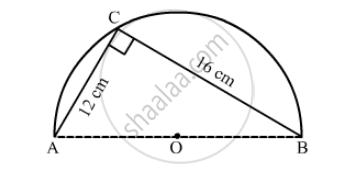
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
The following figure shows two circles with the same center. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).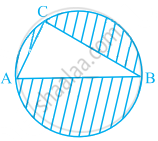
Area of the circle obtained in 196 m2 is ______.
