Advertisements
Advertisements
प्रश्न
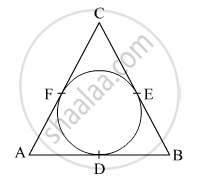
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
उत्तर
Given that AB = 12 cm, BC = 8 cm and AC = 10 cm.
Let, AD = AF = p cm, BD = BE = q cm and CE = CF = r cm
(Tangents drawn from an external point to the circle are equal in length)
`rArr2(p+q+r)`= AB + BC + AC = AD + DB + BE + EC + AF + FC = 30 cm
`rArr p+q+r=15`
AB = AD + DB = p + q = 12 cm
Therefore, r = CF = 15 − 12 = 3 cm.
AC = AF + FC = p + r = 10 cm
Therefore, q = BE = 15 − 10 = 5 cm.
Therefore, p = AD = p + q + r − r − q = 15 − 3 − 5 = 7 cm.
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
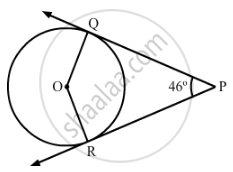
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

The greatest chord of a circle is called its
Find the area of a circle of radius 7 cm.
Use the figure given below to fill in the blank:
Diameter = 2 x ________

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
