Advertisements
Advertisements
Question
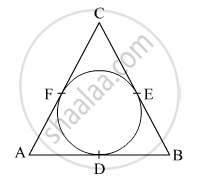
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
Solution
Given that AB = 12 cm, BC = 8 cm and AC = 10 cm.
Let, AD = AF = p cm, BD = BE = q cm and CE = CF = r cm
(Tangents drawn from an external point to the circle are equal in length)
`rArr2(p+q+r)`= AB + BC + AC = AD + DB + BE + EC + AF + FC = 30 cm
`rArr p+q+r=15`
AB = AD + DB = p + q = 12 cm
Therefore, r = CF = 15 − 12 = 3 cm.
AC = AF + FC = p + r = 10 cm
Therefore, q = BE = 15 − 10 = 5 cm.
Therefore, p = AD = p + q + r − r − q = 15 − 3 − 5 = 7 cm.
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
The ratio between the circumference and diameter of any circle is _______
Find the diameter of the circle
Radius = 6 cm
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
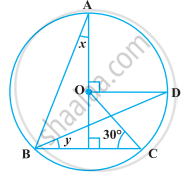
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.