Advertisements
Advertisements
Question
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
Solution
Consider a quadrilateral ABCD touching circle with center O at points E, F, G and H as in figure.
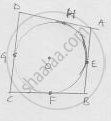
We know that
The tangents drawn from same external points to the circle are equal in length.
1. Consider tangents from point A [AM ⊥ AE]
AH = AE …. (i)
2. From point B [EB & BF]
BF = EB …. (ii)
3. From point C [CF & GC]
FC = CG …. (iii)
4. From point D [DG & DH]
DH = DG …. (iv)
Adding (i), (ii), (iii), & (iv)
(AH + BF + FC + DH) = [(AC + CB) + (CG + DG)]
⇒ (AH + DH) + (BF + FC) = (AE + EB) + (CG + DG)
⇒ AD + BC = AB + DC [from fig.]
Sum of one pair of opposite sides is equal to other.
APPEARS IN
RELATED QUESTIONS
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
The circle which passes through all the vertices of a triangle is called ______.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
