Advertisements
Advertisements
प्रश्न
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
उत्तर
Consider a quadrilateral ABCD touching circle with center O at points E, F, G and H as in figure.
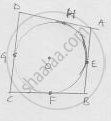
We know that
The tangents drawn from same external points to the circle are equal in length.
1. Consider tangents from point A [AM ⊥ AE]
AH = AE …. (i)
2. From point B [EB & BF]
BF = EB …. (ii)
3. From point C [CF & GC]
FC = CG …. (iii)
4. From point D [DG & DH]
DH = DG …. (iv)
Adding (i), (ii), (iii), & (iv)
(AH + BF + FC + DH) = [(AC + CB) + (CG + DG)]
⇒ (AH + DH) + (BF + FC) = (AE + EB) + (CG + DG)
⇒ AD + BC = AB + DC [from fig.]
Sum of one pair of opposite sides is equal to other.
APPEARS IN
संबंधित प्रश्न
Prove that two different circles cannot intersect each other at more than two points.
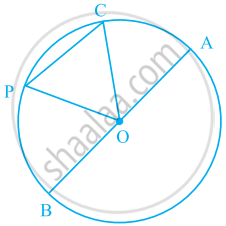
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
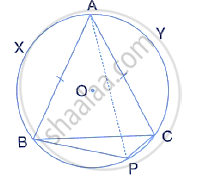
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Draw circle with the radii given below.
4 cm
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
All the radii of a circle are _______________
In the given figure, O is the centre of the circle. Name all chords of the circle.