Advertisements
Advertisements
Question
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
Solution
Radius of a circle (OA) = 15 cm
Distance from centre to the chord (OC) = 12 cm
In the right ΔOAC,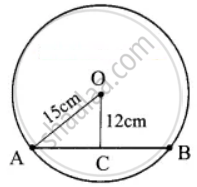
AC2 = OA2 – OC2
= 152 – 122
= 225 – 144
= 81
AC = `sqrt(81)`
= 9
Length of the chord (AB)
= AC + CB
= 9 + 9
= 18 cm.
APPEARS IN
RELATED QUESTIONS
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
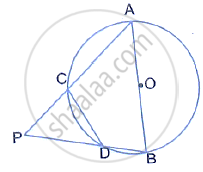
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Find the diameter of the circle
Radius = 8 cm
Find the radius of the circle
Diameter = 30 cm
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.
From the figure, identify three radii.