Advertisements
Advertisements
Question
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
Options
True
False
Solution
This statement is False.
Explanation:
Because, there can be many points D, such that ∠BDC = 60° and each such point cannot be the centre of the circle through A, B and C.
APPEARS IN
RELATED QUESTIONS
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
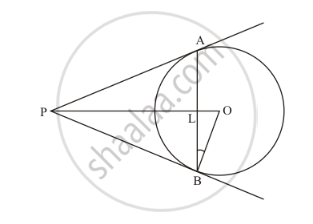
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
Fill in the blank
A continuous piece of a circle is ............... of the circle
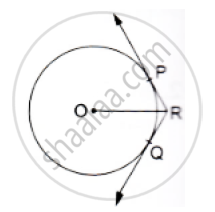
In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
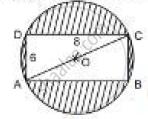
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
From the figure, identify a sector.

