Advertisements
Advertisements
Question
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
Solution
Given: diameter d = 24 m
radius r = `"d"/2`
= `24/2`
= 12 m
Circumference C = 2πr units
= `2 xx 22/7 xx 12`
= `528/7`
= 75.4 m
Tabulating the results
| radius (r) | diameter (d) | Circumference (C) |
| 12 m | 24 m | 75.42 m |
APPEARS IN
RELATED QUESTIONS
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
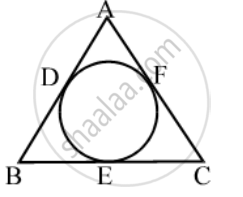
In Fig., if AB = AC, prove that BE = EC
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
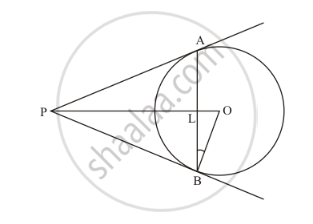
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In the given figure, O is the centre of the circle. Find ∠CBD.

Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
Use the figure given below to fill in the blank:
Tangent to a circle is _______.

Use the figure given below to fill in the blank:
______ is a chord of the circle.

In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is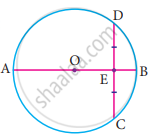
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.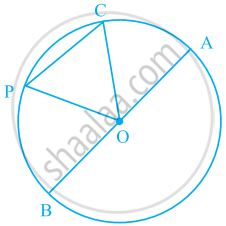
Is every diameter of a circle also a chord?
