Advertisements
Advertisements
प्रश्न
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
उत्तर
Given: diameter d = 24 m
radius r = `"d"/2`
= `24/2`
= 12 m
Circumference C = 2πr units
= `2 xx 22/7 xx 12`
= `528/7`
= 75.4 m
Tabulating the results
| radius (r) | diameter (d) | Circumference (C) |
| 12 m | 24 m | 75.42 m |
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
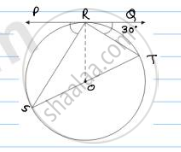
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
ture or false v
The degree measure of a semi-circle is 180°.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

One chord of a circle is known to be 10 cm. The radius of this circle must be
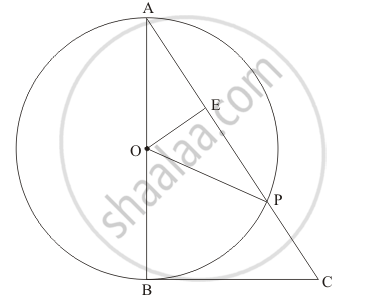
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
The circle which passes through all the vertices of a triangle is called ______.
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
All the radii of a circle are _______________
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c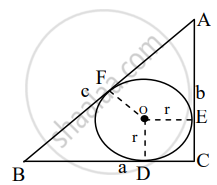
The length of tangent from an external point on a circle is always greater than the radius of the circle.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
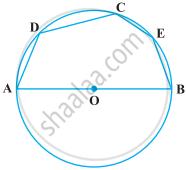
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
