Advertisements
Advertisements
प्रश्न
One chord of a circle is known to be 10 cm. The radius of this circle must be
विकल्प
5 cm
greater than 5 cm
greater than or equal to 5 cm
less than 5 cm
उत्तर
greater than 5 cm
We are given length of a chord to be 10 cm and we have to give information about the radius of the circle.
Since in any circle, diameter of the circle is greater then any chord.
So diameter > 10
⇒ 2r > 10
⇒ r > 5 cm
APPEARS IN
संबंधित प्रश्न
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
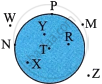 |
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
