Advertisements
Advertisements
प्रश्न
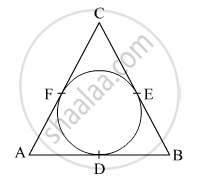
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
उत्तर
Given that AB = 12 cm, BC = 8 cm and AC = 10 cm.
Let, AD = AF = p cm, BD = BE = q cm and CE = CF = r cm
(Tangents drawn from an external point to the circle are equal in length)
`rArr2(p+q+r)`= AB + BC + AC = AD + DB + BE + EC + AF + FC = 30 cm
`rArr p+q+r=15`
AB = AD + DB = p + q = 12 cm
Therefore, r = CF = 15 − 12 = 3 cm.
AC = AF + FC = p + r = 10 cm
Therefore, q = BE = 15 − 10 = 5 cm.
Therefore, p = AD = p + q + r − r − q = 15 − 3 − 5 = 7 cm.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
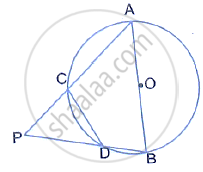
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
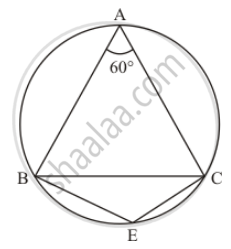
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
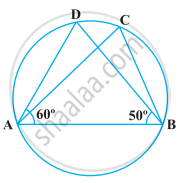
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
